今天是高考的日子! Sheauhaw 决定通过一系列神秘活动为考生祈福, 于是在操场上画出了一个奇怪的图案:
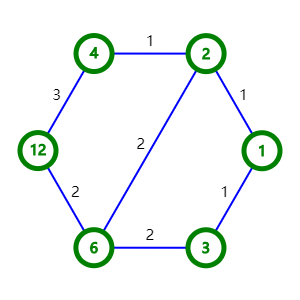
你百思不得其解, Sheauhaw 向你解释的这个图的意义: 今天的考试的幸运数字是 , 于是就可以画一个基于 的幸运法阵. 它是这样制作的:
- 首先生成节点: 法阵中的每个节点都是 的正因子. 显然, 节点不要求是素数, 和 也是节点.
- 之后生成边: 法阵中的任意两个节点 (), 若满足 且 是素数, 那么就会在 和 之间生成一条无向边.
- 最后赋予边权: 连接 () 的边的权值是 相对于 的特有因子个数. 一个数 如果是 的因子, 但不是 的因子, 那么 就是一个 相对于 的特有因子.
例如, 你看到的奇怪图案就是 生成的幸运法阵. 你会发现:
- 这条边的权值是 . 因为 的因子有 , 的因子有 , 于是 相对于 的特有因子有 个, 分别是 .
- 和 之间没有边直接连接, 因为 .
- 和 之间没有边直接连接, 因为 不是素数.
Sheauhaw 解释完这个图的构造后, 说明了这个法阵的应用: 法阵上的两个数字指导着两个行为, 这两个数字之间的关系就尤为重要. Sheauhaw 定义了法阵上两个数字的默契值: 如果 是图上的两个节点, 那么这两点之间最短路的个数称为 之间的默契值 .
由于 Sheauhaw 的幸运占卜计算量极其庞大, 他请你帮他计算 组节点的默契值. 由于数字可能比较大, 他只需要默契值对 取模的值就可以估测两个数字的关系.